最近在尝试复现的 paper Efficient Probabilistic Logic Reasoning with Graph Neural Networks 涉及到了一些关于知识图谱、一阶逻辑和马尔可夫逻辑网相关的基础概念和术语，今天简要梳理了一下做此记录。

一、知识图谱

知识是人类在实践中认识客观世界的结晶。「知识图谱」（Knowledge Graph, KG）是知识工程的重要分支之一，它以符号形式结构化地描述了物理世界中的概念及其相互关系。

知识图谱从萌芽思想的提出到如今已经发展了六十多年，衍生出了许多独立的研究方向，并在众多实际工程项目和大型系统中发挥着不可替代的重要作用。

如今，知识图谱已经成为认知和人工智能日益流行的研究方向，受到学术界和工业界的高度重视。

「知识图谱」是一种结构化的语义知识库，用于迅速描述物理世界中的概念及其相互关系。从结构上来说，知识图谱是由实体和关系组成的多关系图，实体和关系分别被视为节点和不同类型的边。

知识图谱通过对错综复杂的文档的数据进行有效的加工、处理、整合，转化为简单、清晰的“实体，关系，实体”的三元组，最后聚合大量知识，从而实现知识的快速响应和推理。

一般来说，大部分的所谓“知识”都可以化为陈述句的形式。比如“老鼠爱大米”这句话，就可以作为一个知识的最小单元。我们称这样的陈述句为一个「事实」（Fact），此事实可以进一步细分，即拆分成主谓宾三部分：“老鼠”，“爱”，“大米”。我们将“大米”，“老鼠”等客观事物统称为「实体」（Entity），“爱”这个谓词描述了两个实体之间的连接，称为一种「关系」（Relation）。因此一个事实可以认为是描述实体间的一种有向关系，可以表示为一个三元组

$$(h,r,t)\in \mathcal{F}$$

其中 $h$ 被称为「头实体」（Head entity），即“老鼠”，$r$ 是关系，即“爱”，$t$ 被称为「尾节点」（Tail entity），即“大米”。这样一系列的三元组拼接起来，就可以得到所谓的知识图谱。

通常我们将知识图谱本身作为一个数学概念上的图，并将此图形式化定义为 $\mathcal{G}={\mathcal{E},\mathcal{R},\mathcal{F}}$，其中 $\mathcal{E},\mathcal{R},\mathcal{F}$ 分别表示实体集合集合，关系集合和事实集合。

二、一阶逻辑

「一阶逻辑」（first order logic，FOL）也叫一阶谓词演算，允许量化陈述的公式，是使用于数学、哲学、语言学及计算机科学中的一种形式系统。

从一阶逻辑的角度来说，知识图谱中的实体可以被认为是一阶逻辑中的「常量」（constant），而知识图谱中的关系可以被认为是一阶逻辑中的「谓词」（predicate）。每一个谓词都是定义在一系列实体上的一个逻辑函数，取值为真或假。一般来说，谓词是具有不对称性的，即谓词的两个参数是不可对调的。

将常量代入，作为谓词函数的输入参数的过程叫做「基础化」（Grounding）。而得到的谓词就是「基础谓词」（Ground Predicate），而每个基础谓词就是一个取值为真或假的二元随机变量。如果某个知识图谱中有 $M$ 个实体（常量），那么一个有 $d$ 个参数输入的谓词就有 $M^d$ 种方式来使之基础化。对于谓词 $r$ 来说，如果把每一种常数代入方式记为 $a_r$，那么就可以得到一个集合 $A_r={a_r^1,\cdots a_r^{M^d}}$

一旦能够确定某个谓词的结果值，那么就得到了知识图谱中所谓的事实。例如假设 $\text{L}$ 表示了一个谓词，$c,c’$ 各表示了一个常量，那么 $[\text{L}(c,c’)=1]$ 就可以表示一个事实，在一阶逻辑的语境下用 $o$ 表示。

更进一步，几个谓词可以通过逻辑运算符连接得到更加复杂的的二元取值函数。一个典型的逻辑规则格式为

$$f(\cdot):\mathcal{C}\times \cdots \times \mathcal{C}\mapsto {0,1}$$

比如说对于单输入谓词 Smoke 和两输入谓词 Friend 来说，可以得到一个复杂的表述

$$\text{Smoke}(c)\land \text{Friend}(c,c’)\implies\text{Smoke}(c’)\iff
\lnot \text{Smoke(c)}\lor \lnot \text{Friend}(c,c’)\lor \text{Smoke}(c’)$$

称这种二元取值函数为「逻辑规则」（Logic formula）。与谓词的情况类似，如果逻辑规则中所有的谓词的输入都是常量，则称此规则为「基本规则」（Ground Formula）。类似于谓词，逻辑规则基础化时同样存在非常多的常量选取方式。对于逻辑规则 $f$ 而言，每一种常量的选取方式可以记为 $a_f$，由此得到一个集合 $A_f={a_f^1,a_f^2,\cdots }$，一系列逻辑规则就得到了「知识库」（Knowledge Base）。

如果基础化规则集合中每一个规则，那么对每一个规则都一定可以得到确定的真或假的两种结果。此时我们称这样的一种情况叫做「世界」（World），用 $U$ 表示。为了评价一个世界是否符合逻辑，其实只需要将所有规则的结果相与，得到的结果为真，则说明此世界符合逻辑。得到的逻辑函数可以表示为 $L(U)$，这是一个二值函数。

但真实世界比较复杂，因此很断定一个世界是符合逻辑与否的，所以可以将 $L(U)$ 离散化。与其断定一个世界是否符合逻辑，不如评价一个世界有多符合逻辑。因此此时的 $L(U)$ 是一个连续取值的函数，越高表示此世界越符合逻辑。即

$$L(U)=\sum_{i}w_in_i(U)$$

上式表示在某个世界 $U$ 符合逻辑的程度。其中 $w_i$ 是某个规则的权重，表示此规则的成立与否对于世界逻辑性的影响，$n_i$ 表示此规则在这个世界成立的次数。更具体来说，如果对于某个规则来说，其中不同的常量取值 $a_f$ 决定了它发生的次数，即满足公式

$$n_i=\sum_{a_f\in A_f}\phi_f(a_f)$$

其中 $a_f$ 表示此规则的不同的常量取值方式，$\phi_f$ 就是规则所表征的潜在函数关系的一种抽象表示。比如如果 $a_f$ 能够让此规则成立，则 $\phi_f(a_f)$ 为 1，反之为 0。遍历不同的常量选取方式来求和即可得到此规则成立的次数。因此逻辑值公式化为

$$L(U)=\sum_i w_i\sum_{a_f\in A_f}\phi_f(a_f)$$

从概率论的角度来说，对每个世界进行归一化概率运算就求出每个世界为真的概率 $P(U)$，即

$$P(U)=\frac{e^{L(U)}}{\sum_{U’}e^{L(U’)}}$$

上式就表示了某个世界 $U$ 出现的几率。将 $\sum_{U’}e^{L(U’)}$ 记为 $Z(w)$。

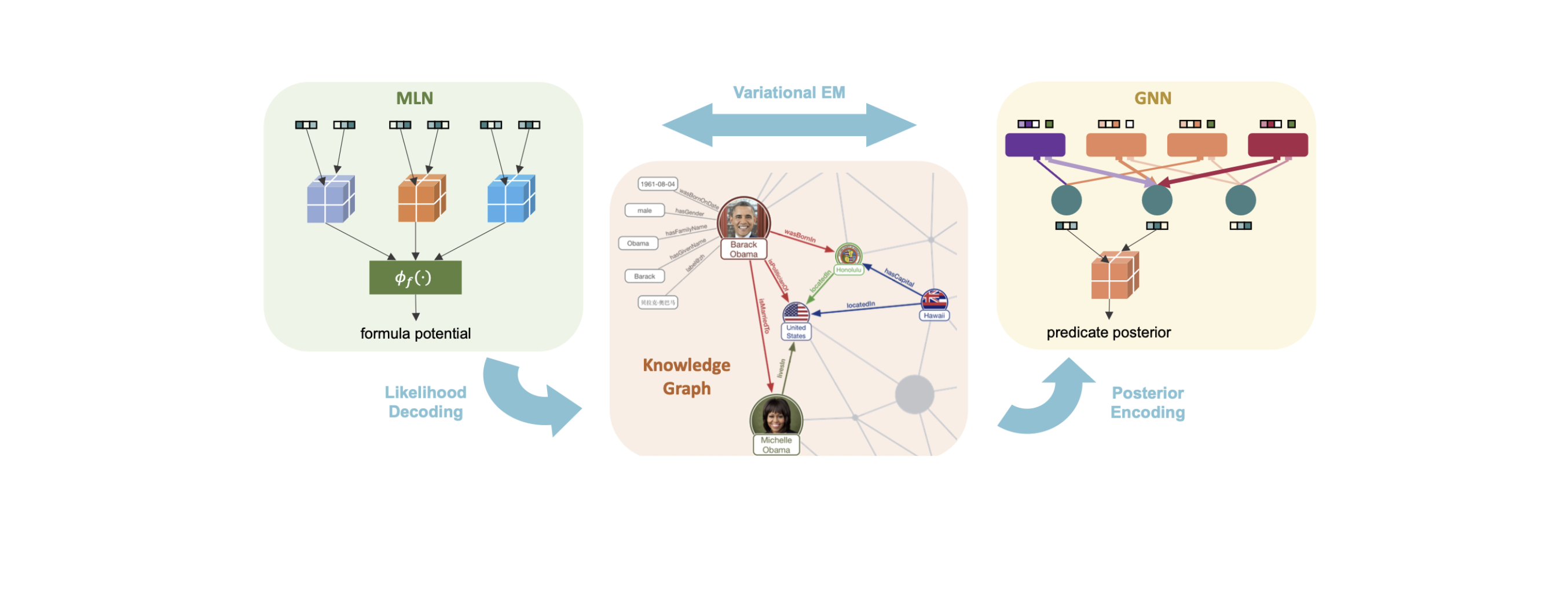
三、马尔可夫逻辑网

马尔可夫逻辑网认为，一阶逻辑中的知识库 $\mathcal{K}$ 可以表示为一个双向图 $\mathcal{G}_\mathcal{K}=(\mathcal{C},\mathcal{O},\mathcal{E})$。它表示一个常量以一条边连接到某个事实。其中 $\mathcal{C}$ 是常量集合，$\mathcal{O}$ 是已知事实集合，称为「因素」（Factor），$\mathcal{E}$ 是边的集合，对于一条从常量 $c$ 到事实 $o$ 的边可以表示为

$$e=(c,o,i)$$

其中 $i$ 表示将常量 $c$ 放在了 $o$ 所代表的谓词的第 $i$ 个参数。在给定逻辑规则的条件下，MLN 就可以被定义为一个所有已知规则 $\mathcal{O}$ 和未知规则 $\mathcal{H}$ 的联合分布

$$P_w(\mathcal{O},\mathcal{H}):=\frac{1}{Z(w)}\exp\left(\sum_{f\in \mathcal{F}}w_f\sum_{a_f\in \mathcal{A}_f}\phi_f(a_f)\right)\tag{1}$$