最近的软件课设需要完成情感分析的任务，潜在狄利克雷分配 LDA 自然是情感分析领域绕不过去的一座丰碑。花了一天时间拜读了原文，并参考了一些其他人的博客，对 LDA 的工作过程有了更清晰的认知，在此作一些简单的笔记分享。

一、简介

「潜在狄利克雷分配主题模型」（Latent Dirichlet Allocation，LDA）是一种利用自然语言和机器学习技术，通过分析非结构化文本数据中的单词信息对一系列文档中的主题进行抽象和聚类，从而实现文本分类的统计模型。

LDA 能够接受一系列文章作为语料库信息，由此创建一系列具有实质性意义的类别，这些类别称为「主题」（Topic），主题的个数 $K$ 由人为事先指定。每个主题下会对应多个单词。LDA 认为每个文档是不同主题的集合，同时每个主题是不同单词的集合。比如预先设置了 $K=3$，对于一个有 12 个单词的文章，LDA 就可以对其进行分为如下架构

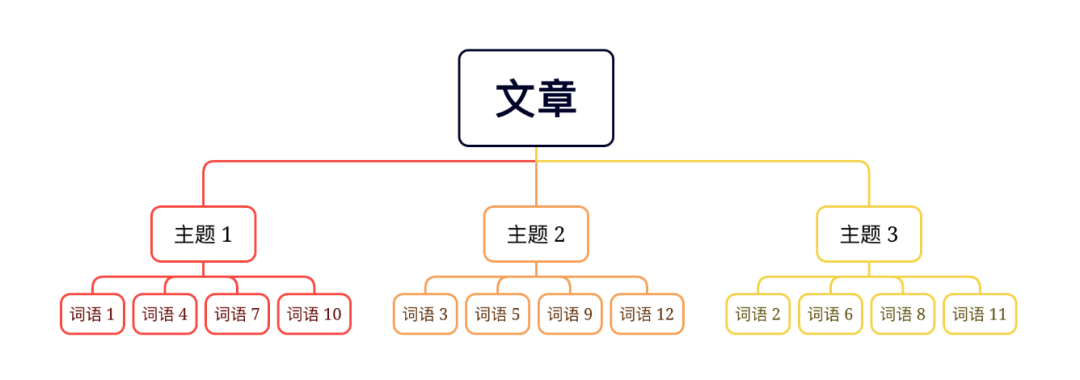
通过 LDA，我们期望的结果是一个可靠的分类器，它能够将若干文档自动编码为一定数量的主题，并输出一个主题分布 $\theta_d$，来表示文章 $d$ 最可能属于规定好的主题中的哪一种。这极大地减少了人为负担和误差。通过分析这些主题，可以做到对大量文章进行关键信息提取，从而进一步分析其中的联系，具体应用有语义分析、文档分类/聚类、文章摘要、社区挖掘等等。

此外，LDA 模型还可以得到每个主题下每个单词出现的概率。从语义上来说，LDA 找到了某一类单词的语义相似性，并将其归类到一起。

二、四大假设

为了更好地展示 LDA 的工作过程，首先对 LDA 各个层次作具体的定义

• 离散数据的最小单元称为「单词」（Word），用 $w$ 表示。各种单词构成的集合称为「词汇表」（Vocabulary），长度为 $V$。根据词汇表，可以对词汇表中出现的任何一个单词进行独热编码，即用一个长度为 $V$ 的向量来表示此单词。比如对于词汇表中的第 $v$ 个单词，则 $w^v=1$ 而其他的 $u\ne v$ 时 $w^u=0$。
• 由 $N$ 个单词组成的有序序列称为「文章」（Document），用 $w=(w_1,w_2,\cdots,w_N)$ 表示。文章中的第 $n$ 个单词则表示为 $w_n$
• 由 $M$ 篇文章构成的集合称为「语料库」（Corpus），用 $D={\text{w}_1,\text{w}_2,\cdots,\text{w}_M}$ 表示。

要理解 LDA，首先需要做几个假设。

1. 文章长度

泊松分布适用于描述在固定时间或空间内稀有事件发生的概率。在文章长度的情境下，我们可以将一个事件定义为一个单词的出现。这种情况下，我们可以假设文章的长度 $N$ 服从泊松分布

$$N\sim Possion(\xi)$$

2. 词主题假设

首先认为，每个单词 $w_n$ 都属于一个主题。比如对于人为设定的分类「艺术 / 科学 / 生活」，单词「蒙娜丽莎」就有很高的可能性属于主题「艺术」。可以用一个向量来表示此单词属于某个主题的第概率，例如 $\begin{bmatrix}0.8&0.1&0.1\end{bmatrix}$ 表示了此单词有大概率属于「艺术」，而只有 0.1 的概率属于另外两种主题。此时将此向量称为「词主题向量」记为 $z_n$。

在这种假设下，词主题向量满足非负性和归一性，因此可以用多项式分布来对此进行词主题向量的建模，即认为 $z_n$ 服从

$$z_{n}\sim Multinomial(\theta)$$

其中 $\theta$ 是一个参数，意思是某篇文章 $\text{w}_n$ 中，随机抽取一个单词，此单词属于某种主题的概率值。

3. 文档主题分布假设

词主题向量的多项式分布参数 $\theta$ 称为「文档-主题分布向量」。对于一篇文章来说，如果我们拿到了它的 $\theta$，也就意味着我们掌握了它的主题分布情况，这就是我们所追求的目标——对文本进行分类。

贝叶斯学派认为，此时的 $\theta$ 本身虽然是参数，但是同样可以认为是随机变量，其分布符合参数为 $\alpha$ 的 Dirichlet 分布，即对于某篇文章 $\text{w}_n$，有

$$\theta\sim Dirichlet(\alpha)$$

这里的 $\alpha$ 是一个参数，但此参数我们无法准确获得，只能通过训练和学习去尝试估计。因此 $\alpha$ 也可以认为是一种「知识」

4. 单词向量假设

我们认为，LDA 可以在已知某个单词的词主题向量的前提下，尝试「生成」这个单词 $w_n$，这是上文提到的对单词的独热编码，即「单词向量」。

所谓的生成单词，其实就是在讨论，如果已知这个地方的单词主题是什么，而且知道这个主题意味着有哪些单词可以填，我们就知道这个时候该填什么单词。

比如已知某处单词极大概率是「艺术」主题，而生成器又有先验知识，它知道「艺术」的语境下，「蒙娜丽莎」「达芬奇」出现的概率大于「万有引力」「牛顿」，所以它就会倾向于在此处生成「蒙娜丽莎」或「达芬奇」。

用数学的语言描述，单词向量的概率分布是一个条件概率密度，即在已知单词的主题分布条件 $z_n$ 下，满足参数为 $\beta$ 的多项分布，可以表示为

$$w_n\sim p(w_n|z_n,\beta)$$

其中，$\beta$ 是一个参数，同样可以理解成所谓的生成器的先验知识，即「在什么语境下该填什么词」。

在上面四种假设中，我们用到了两个参数 $\alpha$ 和 $\beta$。其中，$\alpha$ 是一个长度为主题数 $k$ 的一个向量，而 $k$ 是提前指定好的，所以 $\theta$ 的长度也就等于主题数 $k$。其次，$\beta$ 是一个形状为 $k\times V$ 的矩阵，它的每一个元素 $\beta_{ij}$ 表示的就是主题为 $z_i$ 的情况下，此单词为为 $w_j$ 的概率。

三、生成语料库的概率推导

对 $\theta$ 进行明确的定义。根据 Dirichlet 分布的数学公式

$$p(\theta|\alpha)=\frac{\Gamma(\sum_{i=1}^k\alpha_i)}{\prod_{i=1}^k\Gamma(\alpha_i)}\prod_{i=1}^k\theta_i^{\alpha_i-1}\tag{1}$$

理论上来说，LDA 能够凭借主题信息生成单词，那么能否进而生成整篇文章甚至一个语料库呢？我们先从文章的角度来分析。

假定对于某篇长度为 $N$ 的文章，$N$ 个词主题向量 $z_n$ 的集合可以记为 $\text{z}$，单词向量 $w_n$ 的集合记为 $\text{w}$。如果已知了 $\alpha$ 和 $\beta$，就可以根据概率论的基本知识得到，其文档-主题分布向量为 $\theta$，单词向量集合为 $\text{z}$，单词向量为 $\text{w}$ 的概率可以表示为

$$p(\theta, \text{w},\text{z}|\alpha,\beta)=p(\theta|\alpha)\prod_{n=1}^Np(z_n|\theta)p(w_n|z_n,\beta)\tag{2}$$

上式用通俗的语言来说就是，首先通过先验知识 $\alpha$ 估计出某篇文章的主题 $\theta$ ，然后对于每一篇文章而言，用 $\theta$ 估计出这篇文章每个单词可能属于的主题。如果对于第 $n$ 个单词，其主题分布为 $z_n$，就可以根据先验知识 $\beta$ 和这个单词可能的主题 $z_n$ 生成这个单词本身 $w_n$

如果对 $\theta$ 积分，同时对 $z$ 求和，则可以得到

$$P(\text{w}|\alpha,\beta)=\int p(\theta|\alpha)\left(\prod_{n=1}^N\sum_{z_n}p(z_n|\theta)p(w_n|z_n,\beta)\right)d\theta\tag{3}$$

此时的式子看起来夸张了不少，让我们逐步分析：

• 最内部，对 $z_n$ 求和后的结果，相当于是对于某一个单词而言，无论其主题可能是什么，最后单词本身的分布概率。换而言之，对于过程 $\theta \to z_n\to w_n$ 而言，我们“整合”了 $z_n$ 这个过程，求和式表示了不需要了解单个单词属于什么主题，直接从文章的主题 $\theta$ 得到每个单词本身 $w_n$ 的分布情况。
• 求连乘的结果，就是在对整篇文章所有的单词进行估计。换而言之，就是给定 $\theta$ 时，单词向量集合 $\text{w}$，即整篇文章的结果。
• 而再将此结果对 $\theta$ 积分，得到的结果就是只需要给定参数 $\alpha,\beta$，LDA 生成某篇文章 $\text{w}$ 的概率。

经过「求和-连乘-积分」三个步骤，我们只需要先验知识 $\alpha$ 和 $\beta$ 就可以直接生成一篇文章。进一步，文章的集合就是语料库，对生成文章的概率再连乘，就得到 LDA 生成整个语料库 $D$ 的概率

$$p(D|\alpha,\beta)=\prod_{d=1}^M\int p(\theta_d|\alpha)\left(\prod_{n=1}^N\sum_{z_{dn}}p(z_{dn}|\theta)p(w_{dn}|z_{dn},\beta)\right)d\theta$$

综上，LDA 生成一个语料库的过程可以表示为下图

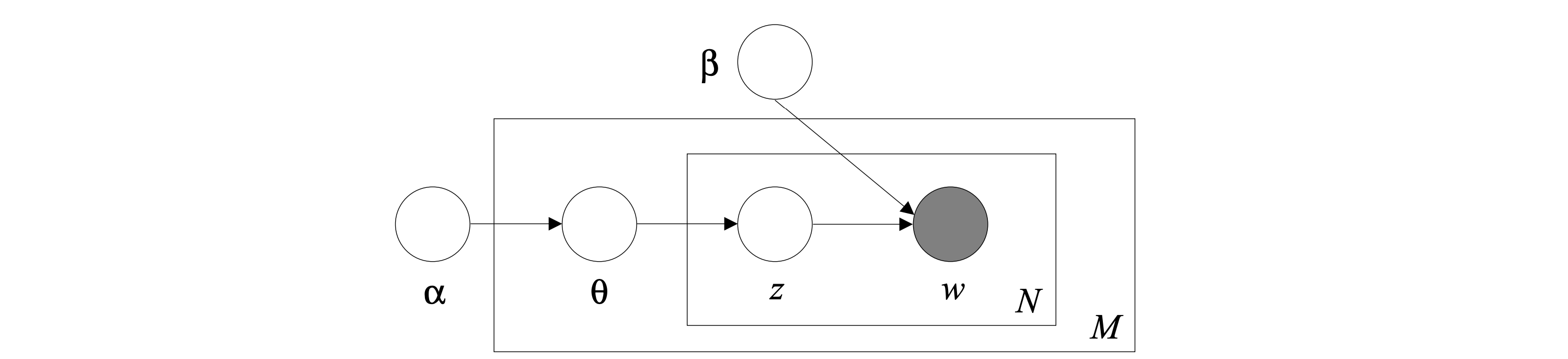
可以看到，LDA 的生成是分三个层级的。其中参数 $\alpha$ 和 $\beta$ 是语料库级别的参数，$\theta$ 是文章级别的参数，而 $z,w$ 是单词级别的参数。

四、主题推断

为了将 LDA 模型用于主题的推断，我们执行的就是生成语料库的「逆过程」——已知参数 $\alpha,\beta$ 和文章 $\text{w}$，得到各个文章可能属于的主题 $\theta$ 和各个单词可能属于的主题 $\text{z}$。根据 Bayes 公式，此后验概率可以表示为

$$p(\theta,\text{z}|\text{w},\alpha,\beta)=\frac{p(\theta,\text{z},\text{w}|\alpha,\beta)}{p(\text{w}|\alpha,\beta)}$$

再来强调一下各项的实际意义。

• 所有项的条件中都有 $\alpha,\beta$，这是一个文章生成器训练得到的先验知识。
• 等号左边的 $p(\theta,\text{z}|\text{w},\alpha,\beta)$ 表示生成器在已知文章 $\text{w}$ 的情况下，对这篇文章的分类 $\theta,\text{z}$，这就是我们为了实现「文本分类」这一任务所需要计算的
• 等号右边，$p(\text{w}|\alpha,\beta)$ 生成器直接生成出我们输入的这篇文章 $\text{w}$ 的概率。
• 另一方面，$p(\theta,\text{z},\text{w}|\alpha,\beta)$ 表示生成器不仅生成出我们需要的已知文章，还恰好属于我们需要的类别的概率。

我认为这个 Bayes 公式体现了 LDA 的精髓。而且这一公式看起来非常的反直觉，我们输入了一篇文章 $\text{w}$，然后居然指望生成器在只有先验知识的情况下，生成出一篇完全一模一样的文章。但这确实是 Bayes 理论告诉我们的——理论上只要我们能把这两个概率求出来就行。

其中 $p(\theta,\text{z},\text{w}|\alpha,\beta)$ 我们已知
$$p(\theta, \text{w},\text{z}|\alpha,\beta)=p(\theta|\alpha)\prod_{n=1}^Np(z_n|\theta)p(w_n|z_n,\beta)\tag{2}$$
而 $p(\text{w}|\alpha,\beta)$ 的计算就比较棘手了。根据 (3) 式：

$$P(\text{w}|\alpha,\beta)=\int p(\theta|\alpha)\left(\prod_{n=1}^N\sum_{z_n}p(z_n|\theta)p(w_n|z_n,\beta)\right)d\theta\tag{3}$$

其中 $p(\theta|\alpha)$ 可以用 Dirichlet 定义式表示

$$p(\theta|\alpha)=\frac{\Gamma(\sum_{i=1}^k\alpha_i)}{\prod_{i=1}^k\Gamma(\alpha_i)}\prod_{i=1}^k\theta_i^{\alpha_i-1}\tag{1}$$

因此原式化为

$$p(\text{w}|\alpha,\beta)=\int \frac{\Gamma(\sum_{i=1}^k\alpha_i)}{\prod_{i=1}^k\Gamma(\alpha_i)}\prod_{i=1}^k\theta_i^{\alpha_i-1}\left(\prod_{n=1}^N\sum_{z_n}p(z_n|\theta)p(w_n|z_n,\beta)\right)d\theta$$

将与 $\theta$ 无关的部分提出积分

$$p(\text{w}|\alpha,\beta)=\frac{\Gamma(\sum_{i=1}^k\alpha_i)}{\prod_{i=1}^k\Gamma(\alpha_i)}\int \left(\prod_{i=1}^k\theta_i^{\alpha_i-1}\right)\left(\prod_{n=1}^N\sum_{z_n}p(z_n|\theta)p(w_n|z_n,\beta)\right)d\theta$$

对于求和项中的 $p(w_n|z_n,\theta)$，这里可以用一个小技巧将其展开。根据 $\beta$ 的定义，$\beta_{ij}$ 表示的是主题为 $z_i$ 的情况下，此单词为为 $w_j$ 的概率。如果当前词语的主题为 $z_i$，则

$$p(w_j|z_i,\beta)=\prod_{j=1}^V(\beta_{ij})^{w_n^j}$$

由于 $w_n$ 表示的是第 $n$ 个词语的独热编码，因此只有当 $w_n^j$ 对应的是为 1 的项时，$(\beta_{ij})^{w_n^j}$ 的值才不为 1，因此这个连乘式得到的结果，恰恰就是在主题 $z_n$ 下，词语为 $w_n$ 的概率。因此原式化为

$$p(\text{w}|\alpha,\beta)=\frac{\Gamma(\sum_{i=1}^k\alpha_i)}{\prod_{i=1}^k\Gamma(\alpha_i)}\int \left(\prod_{i=1}^k\theta_i^{\alpha_i-1}\right)\left(\prod_{n=1}^N\sum_{z_n}p(z_n|\theta)\prod_{j=1}^V(\beta_{ij})^{w_n^j}\right)d\theta$$

$p(z_n|\theta)$ 描述的是在给定文章主题向量 $\theta$ 的情况下，$z_n$ 的分布情况。而 $\theta_i$ 表示的就是此时 $z_n^i=1$ 的概率。那么结合 $\beta$ 的定义，只有当 $w_n^j$ 对应的是为 1 的项时，$(\theta_i\beta_{ij})^{w_n^j}$ 的值才不为 1，因此这个连乘式得到的结果，恰恰就是对于主题 $\theta_i$ 而言，词语为 $w_n$ 的概率。如果将这 $k$ 个 $\theta_i$ 求和，即可得到下式

$$p(\text{w}|\alpha,\beta)=\frac{\Gamma(\sum_i\alpha_i)}{\prod_i\Gamma(\alpha_i)}\int\left(\prod_{i=1}^k\theta_i^{\alpha_i-1}\right)\left(\prod_{n=1}^N\sum_{i=1}^k\prod_{j=1}^V(\theta_i\beta_{ij})^{w_n^j}\right)d\theta$$

由于 $\theta_i$ 和 $\beta_{ij}$ 存在耦合，这个函数是难以直接计算的。但是 Dickey 在 1983 年的研究表明，这个复杂的函数可以视为在狄利克雷分布的一个特定扩展下的期望值，这个扩展可以用特殊的超几何函数来表示。这意味着虽然直接计算这个函数是困难的，但可以通过理解其作为某种概率分布下的期望来间接处理。在此文中，我们不对这部分内容作详细展开。

五、变分推断

在本部分内容中，我们讨论基于凸性的变分推断是如何在 LDA 中得到应用的。

「基于凸性的变分推断」（Convexity-Based Variational Inference）的基本思想就是利用 Jensen 不等式来获得一个对数似然的下界。本质上，这是考虑一组由一系列变分参数索引的下界。这些变分参数是通过一个旨在找到尽可能紧密的下界的优化过程来选择的。受限于数学基础薄弱，笔者无法对这部分内容作详细展开，在此仅给出 LDA 变分推断算法的伪代码

• initialize $\phi_{ni}^0:=1/k$ for all $i$ and $n$
• initialize $\gamma_{i}:=\alpha +N/k$ for all $i$
• repeat
• for $n = 1$ to $N$
  • for $i = 1$ to $k$
  • $\phi_{ni}^{t+1}=\beta_{i{W_n}}\exp(\Psi(\gamma_i^t))$
  • normalize $\phi_n^{t+1}$ to sum to 1
• $\gamma^{t+1}:=\alpha+\sum_{n=1}^N\phi_n^{t+1}$
• until convergence

其中 $\phi$ 和 $\gamma$ 是变分分析的重要参数。通过以上迭代过程，可以找出 $\phi$ 和 $\gamma$ 的最优值，从而估计出对数似然函数的下界。具体的应用在下面的参数估计给出。

六、参数估计

「参数估计」（Parameter Estimation）的目标，就是给定一个语料库 $D={\text{w}_1,\text{w}_2,\cdots,\text{w}_M}$，找出最合适的 $\alpha,\beta$ 参数，使得数据的似然函数最大。在机器学习的语境下，此过程就可以认为是对 LDA 模型进行训练以达到预期效果。对数似然函数可以表示为

$$\mathscr{l}(\alpha,\beta)=\sum_{d=1}^M\log p(\text{w}_d|\alpha,\beta)$$

正如上文所说，$p(\text{w}|\alpha,\beta)$ 是难以直接计算的。由于变分推断可以给出它的一个可计算的下界，因此我们可以由此来估算此对数似然函数。通过最大化这个下界，可以近似地估计 LDA 模型的 $\alpha$ 和 $\beta$。此过程类似于经验贝叶斯估计（empirical Bayes estimates），并且使用一种交替的变分 EM（Expectation-Maximization）过程实现。

变分 EM 算法包括两个步骤，E 步骤（Expectation step）和 M 步骤（Maximization step）。

• E 步骤：对于每篇文章，找到变分参数 $\gamma$ 和 $\phi$ 的最优值。
• M 步骤：在变分参数固定的情况下，最大化对数似然的下界，从而对模型参数 $\alpha$ 和 $\beta$ 进行优化。这相当于在近似后验下，对每个文档计算最大似然估计和期望的充分统计量。

这两个步骤交替进行，直到对数似然的下界收敛。理论证明，条件多项式参数 $\beta$ 的 $M$ 步更新过程可以解析地表示为

$$\beta_{ij}\propto \sum_{d=1}^M\sum_{n=1}^{N_d}\phi_{dni}^*w_{dn}^i$$

同样地，对狄利克雷参数 $\alpha$ 的 $M$ 步更新过程可以通过一个有效的 Newton-Raphson 方法实现，其中 Hessian 矩阵的逆可以在线性时间内计算。

七、Gibbs 采样迭代

Gibbs 采样同样是一种可行的迭代过程。其思想在于，对于每个词 $w_n$，基于其分配的主题的情况以及所有文档中相同词倍分配给此主题的情况，计算 $z_n$ 属于主题 $i$ 的条件概率。对于第 $d$ 篇文档的第 $n$ 的单词有

$$P(z_{d,n}^i=\theta_i|z_{-d,n}, w_{d,n},\alpha,\beta)\approx \frac{n_{d,i}^{(-d,n)}+\alpha_i}{\sum_{i’}(n_{d,i’}+\alpha_{i’})}\times \frac{n_{i,w_{d,n}}^{(-d,n)}+\beta_{w_{d,n}}}{\sum_w(n_{i,w}^{-d,n}+\beta_w)}$$

其中 $n_{d,i}^{-d,n}$ 表示文档 $d$ 中分配给主题 $i$ 的词的数量，不包括当前词 $w_{d,n}$，$n_{k,w_{d,n}}^{-d,n}$ 表示所有文档中分配给 $k$ 且词为 $w_{d,n}$ 的数量，不包括当前文档的当前词。

因此迭代过程可以表示为

• 随机初始化：对于每个文档 $\text{w}_n$ 中的每个词 $w_n$，随机分配一个来自预设主题集的主题 $z_n$。这种随机分配作为迭代过程的起始点。
• 迭代更新
• 对于语料库中的每个文档 $\text{w}_n$
  • 对于文档库中的每个单词 $w_n$
  • 首先从当前主题分配中移除 $z_n$，即暂时不考虑当前词的主题分配，这意味着在计算新的主题分配时，这个词被视为不存在。
  • 然后在此基础上，对每个可能的主题 $\theta_i$，计算将 $w_n$ 分配到此主题的条件概率。
  • 根据这些条件概率，重新为 $w_n$ 选择一个主题分配 $z_n$
• 重复直至收敛

收敛的判断同样可以用似然函数进行判断

$$\mathscr{l}(\alpha,\beta)=\sum_{d=1}^M\log p(\text{w}_d|\alpha,\beta)$$

这个方法在计算上相对简单，不需要复杂的数学推导，但可能需要大量的迭代来达到收敛。特别适用于文档集不是特别大，且主题数量不是特别多的情况。

八、应用

经过参数推断后，如果对语料库生成了最佳的 $\alpha,\beta$，就可以得到各个文章可能属于的主题 $\theta$ 和各个单词可能属于的主题 $\text{z}$。这意味着 LDA 具有识别文档集中的隐含主题的能力，这有助于对文档进行分类或聚类。例如，新闻文章可以根据其内容自动分类为政治、经济、体育等主题。在推荐系统中，LDA 可以帮助理解用户的兴趣和偏好。通过分析用户过去阅读的文章的主题，可以推荐相似主题的新文章。

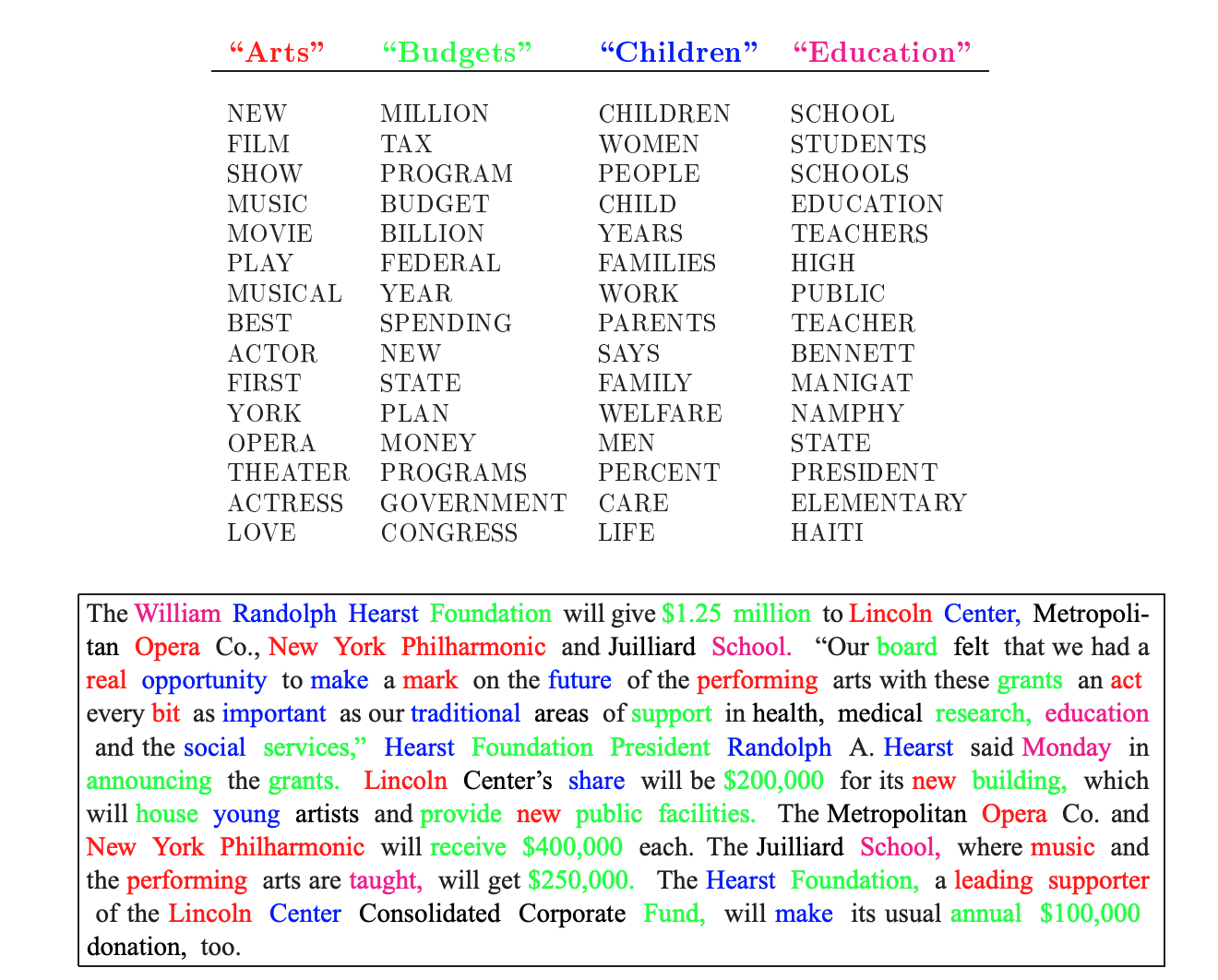
有意思的是，虽然 LDA 本身不直接进行情感分析，但它可以帮助识别表达特定情感的主题，进而用于辅助情感分析的任务。在社交媒体分析中，LDA可以用来识别关于特定事件或话题的讨论主题，从而帮助了解公众的观点和兴趣。